This is more a tutorial write up and less a puzzle. So without further ado here you go.
Q: You have a certain amount of money. You are playing a coin tossing game where you know that the probability of you winning in a certain toss is 'p'. You can keep tossing this coin as long as you want. How much of your money should you bet on each toss to maximize your overall returns.
The Kelly Capital Growth Investment Criterion: Theory and Practice (World Scientific Handbook in Financial Economic Series)
A: This problem was first described by J.L. Kelly in 1956 and is known as the "Kelly Criteria". It provides a direct formula for what fraction of your money you should be betting. The interesting thing here is that the Kelly criteria has been used in gambling and investment strategists (including the likes of Warren Buffet). So how does one arrive at that formula? The following is an easy and simple explanation for it.
Fortune's Formula: The Untold Story of the Scientific Betting System That Beat the Casinos and Wall Street
Assume:
Initial amount of money = C
Payout if you win = α
Loss if you lose = β
Probability of winning = p
Fraction of money to bet = f
A key point to note is that sequence of wins don't matter here. For example if you win in the first throw and lose in the second, your bankroll would proceed as shown in the figure below.
Notice, all that happens after a win (or loss) is the appearance of a multiplicative factor of (1 + (1+ α)f) or (1 - (1 - β)f). So the final bankroll after a win-loss scenario and a loss-win scenario is the same:
If you were to play the game 'N' times you would expect to win 'pN' times. Thus your final bankroll will be
Simplifying it and taking logarithms yields
It is intuitive to see that G is the average yield per play. If we maximize G, that 'f' would lead us to the best strategy. To get to that 'f', we first find the derivative w.r.t G and set it to zero. (I leave it to the reader to verify that the second derivative is negative, hence the solution to the first derivative yields a maximum)
$$
\frac{\partial G}{\partial f} = \frac{p(1+\alpha)}{1 + (1 + \alpha)f} - \frac{(1-p)(1-\beta}{(1 - (1 - \beta)f} = 0
$$
The above equation on simplification yields the optimal 'f' as
The above result is a more generalized version of the Kelly criteria.
In order to test this let us try to generate some simulations around a fixed value of (α,β) and other parameters. The chart below shows the variation of returns using the Kelly criteria vs a simple strategy. The parameters chosen were,
Initial bankroll = $100
Fixed bet size = $6
Win Probability = 55%
Returns if winning = 5%
Loss if losing = 1%
Number of games played = 500
The red line is the returns from the Kelly criteria while the blue line is from the simple fixed bet strategy. If you run the simulation over and over again, the charts will look slightly different, and the Kelly criterion strategy would typically tend to be more volatile or even under perform the simple betting strategy. Also notice, the Kelly strategy starts converting much better when it is on a winning streak and likewise loses faster when it is on a losing streak.
In the real world (say stock trading or in Poker games) there are a lot more parameters at play that just a win loss strategy. Using purely the Kelly strategy may not be a good idea. This is meant to be a guide on a rational asset allocation strategy. A popular and much used idea is to use what is known as "Fractional Kelly". This approach takes a fraction of what the Kelly criteria suggests.
The R code used to generate the chart above is shown below. Due to the stochastic nature, a rerun may not generate the same chart as above.
If you are looking to buy some books in probability here are some of the best books to learn the art of Probability
Q: You have a certain amount of money. You are playing a coin tossing game where you know that the probability of you winning in a certain toss is 'p'. You can keep tossing this coin as long as you want. How much of your money should you bet on each toss to maximize your overall returns.
The Kelly Capital Growth Investment Criterion: Theory and Practice (World Scientific Handbook in Financial Economic Series)
A: This problem was first described by J.L. Kelly in 1956 and is known as the "Kelly Criteria". It provides a direct formula for what fraction of your money you should be betting. The interesting thing here is that the Kelly criteria has been used in gambling and investment strategists (including the likes of Warren Buffet). So how does one arrive at that formula? The following is an easy and simple explanation for it.
Fortune's Formula: The Untold Story of the Scientific Betting System That Beat the Casinos and Wall Street
Assume:
Initial amount of money = C
Payout if you win = α
Loss if you lose = β
Probability of winning = p
Fraction of money to bet = f
A key point to note is that sequence of wins don't matter here. For example if you win in the first throw and lose in the second, your bankroll would proceed as shown in the figure below.
Notice, all that happens after a win (or loss) is the appearance of a multiplicative factor of (1 + (1+ α)f) or (1 - (1 - β)f). So the final bankroll after a win-loss scenario and a loss-win scenario is the same:
If you were to play the game 'N' times you would expect to win 'pN' times. Thus your final bankroll will be
Simplifying it and taking logarithms yields
It is intuitive to see that G is the average yield per play. If we maximize G, that 'f' would lead us to the best strategy. To get to that 'f', we first find the derivative w.r.t G and set it to zero. (I leave it to the reader to verify that the second derivative is negative, hence the solution to the first derivative yields a maximum)
\frac{\partial G}{\partial f} = \frac{p(1+\alpha)}{1 + (1 + \alpha)f} - \frac{(1-p)(1-\beta}{(1 - (1 - \beta)f} = 0
$$
The above equation on simplification yields the optimal 'f' as
The above result is a more generalized version of the Kelly criteria.
In order to test this let us try to generate some simulations around a fixed value of (α,β) and other parameters. The chart below shows the variation of returns using the Kelly criteria vs a simple strategy. The parameters chosen were,
Initial bankroll = $100
Fixed bet size = $6
Win Probability = 55%
Returns if winning = 5%
Loss if losing = 1%
Number of games played = 500
In the real world (say stock trading or in Poker games) there are a lot more parameters at play that just a win loss strategy. Using purely the Kelly strategy may not be a good idea. This is meant to be a guide on a rational asset allocation strategy. A popular and much used idea is to use what is known as "Fractional Kelly". This approach takes a fraction of what the Kelly criteria suggests.
The R code used to generate the chart above is shown below. Due to the stochastic nature, a rerun may not generate the same chart as above.
If you are looking to buy some books in probability here are some of the best books to learn the art of Probability
| Book | Notes/Comments |
|---|---|
| Fifty Challenging Problems in Probability with Solutions (Dover Books on Mathematics) | This book is a great compilation that covers quite a bit of puzzles. What I like about these puzzles are that they are all tractable and don't require too much advanced mathematics to solve. |
| Introduction to Algorithms | This is a book on algorithms, some of them are probabilistic. But the book is a must have for students, job candidates even full time engineers & data scientists |
| Introduction to Probability Theory | Overall an excellent book to learn probability, well recommended for undergrads and graduate students |
| An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd Edition | This is a two volume book and the first volume is what will likely interest a beginner because it covers discrete probability. The book tends to treat probability as a theory on its own |
| The Probability Tutoring Book: An Intuitive Course for Engineers and Scientists (and Everyone Else!) | A good book for graduate level classes: has some practice problems in them which is a good thing. But that doesn't make this book any less of buy for the beginner. |
| Introduction to Probability, 2nd Edition | A good book to own. Does not require prior knowledge of other areas, but the book is a bit low on worked out examples. |
| Bundle of Algorithms in Java, Third Edition, Parts 1-5: Fundamentals, Data Structures, Sorting, Searching, and Graph Algorithms (3rd Edition) (Pts. 1-5) | An excellent resource (students, engineers and even entrepreneurs) if you are looking for some code that you can take and implement directly on the job |
| Understanding Probability: Chance Rules in Everyday Life | This is a great book to own. The second half of the book may require some knowledge of calculus. It appears to be the right mix for someone who wants to learn but doesn't want to be scared with the "lemmas" |
| Data Mining: Practical Machine Learning Tools and Techniques, Third Edition (The Morgan Kaufmann Series in Data Management Systems) | This one is a must have if you want to learn machine learning. The book is beautifully written and ideal for the engineer/student who doesn't want to get too much into the details of a machine learned approach but wants a working knowledge of it. There are some great examples and test data in the text book too. |
| Discovering Statistics Using R | This is a good book if you are new to statistics & probability while simultaneously getting started with a programming language. The book supports R and is written in a casual humorous way making it an easy read. Great for beginners. Some of the data on the companion website could be missing. |
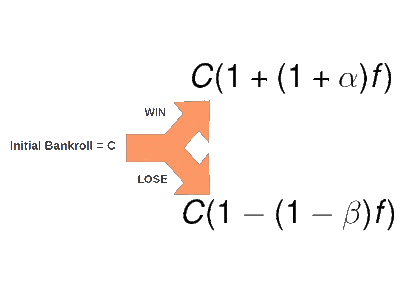





error in dg/df. Should be p(1+alpha) not p in the first numerator.
ReplyDeleteCorrected. Thanks for pointing out
Delete