Often times a lot of people working with data are trying to create an index of some sort. Something that captures a set of key business metrics. If you are a site (or an app) you want to create some sort of an engagement index, which if trending up implies good things are happening, bad if it is trending down. The creators of such metrics (think analysts) tend to prefer a weighted arithmetic mean of the influencing factors. If the influencing factors are f1,f2, f3 (say) with weights w1, w2, w3 then the index would be computed as
However, what does not get factored in are the final consumers of the index (think product managers) and there could be many. They will invariably try to check it with something else they have handy. For example, if clicks on a site went up 20% the index may be up by just 5% (say) or vice-versa. If resources are being allocated based on the movement of such an index, it will invariably lead to contention on what is the right weighting to be given to each factor.
This is meant to be a short write up on some really cool features of the geometric mean. The geometric mean is not meant to replace a simple arithmetic mean based index, but it is definitely worth the thought. To illustrate what this aspect is, lets take a look at a simple two feature index. If the features are X and Y the arithmetic mean index can be represented as
To see how it responds to changes, lets take the derivative.
Clearly the derivative is dependent on the chosen weight. Lets see what happens when we choose the geometric mean.
Again, to see how it responds to change, lets take the derivative.
which can be further simplified to
i.e. the percentage change in the index is directly proportional to the percentage change in the feature.
Note, there are no hand chosen weights here. A five percent change in one of the influencing factors will result in a proportional percent change in the index. Extremely useful !
Yet another aspect consumers like to quantify is growth. If the index went up by x1 and x2 in consecutive years, what is the average quarterly/annual growth? If we took it as the average of x1 and x2, then the growth after two years (say) would be estimated as
Contrast that to the actual growth
Clearly some terms cancel out. We are left comparing
Notice one of them is the arithmetic mean and the other is the geometric mean. We also know from a well established theorem that the arithmetic mean is always greater than the geometric mean described here. So we would always end up overestimating the growth!
So how would we choose a value to project as an average growth rate? We are looking for a beta in the below equation
Yet again stating the average growth as the geometric mean gives the end user a handy metric to work with.
If you are interested in learning probability here are a set of good books to choose and buy from.
However, what does not get factored in are the final consumers of the index (think product managers) and there could be many. They will invariably try to check it with something else they have handy. For example, if clicks on a site went up 20% the index may be up by just 5% (say) or vice-versa. If resources are being allocated based on the movement of such an index, it will invariably lead to contention on what is the right weighting to be given to each factor.
This is meant to be a short write up on some really cool features of the geometric mean. The geometric mean is not meant to replace a simple arithmetic mean based index, but it is definitely worth the thought. To illustrate what this aspect is, lets take a look at a simple two feature index. If the features are X and Y the arithmetic mean index can be represented as
To see how it responds to changes, lets take the derivative.
Clearly the derivative is dependent on the chosen weight. Lets see what happens when we choose the geometric mean.
Again, to see how it responds to change, lets take the derivative.
which can be further simplified to
The result is a useful derivable condition
Note, there are no hand chosen weights here. A five percent change in one of the influencing factors will result in a proportional percent change in the index. Extremely useful !
Yet another aspect consumers like to quantify is growth. If the index went up by x1 and x2 in consecutive years, what is the average quarterly/annual growth? If we took it as the average of x1 and x2, then the growth after two years (say) would be estimated as
Clearly some terms cancel out. We are left comparing
Notice one of them is the arithmetic mean and the other is the geometric mean. We also know from a well established theorem that the arithmetic mean is always greater than the geometric mean described here. So we would always end up overestimating the growth!
So how would we choose a value to project as an average growth rate? We are looking for a beta in the below equation
Yet again stating the average growth as the geometric mean gives the end user a handy metric to work with.
If you are interested in learning probability here are a set of good books to choose and buy from.







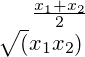

Comments
Post a Comment